valued mammal

Blog

Casual research running -mempoolfullrbf

Prelude

I published results from the first iteration of this mini-study in Nov 2023 which I encourage anyone to read as a short primer. In this post I’ll share the remaining findings as I wind down the second phase of the study and offer some closing thoughts and ideas for the future.

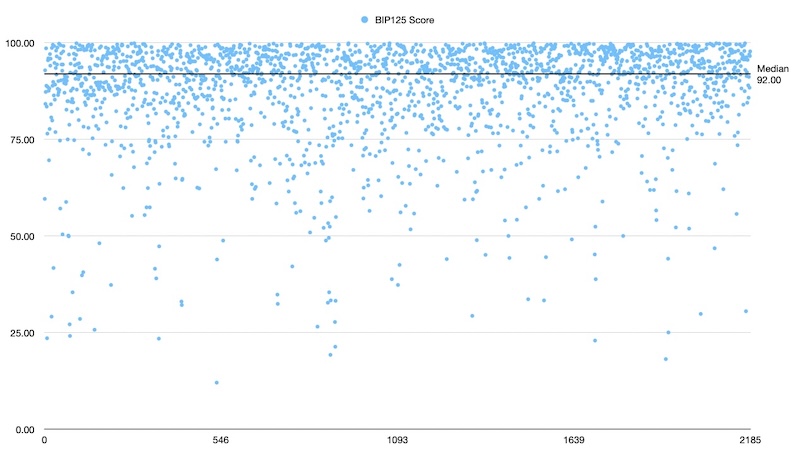
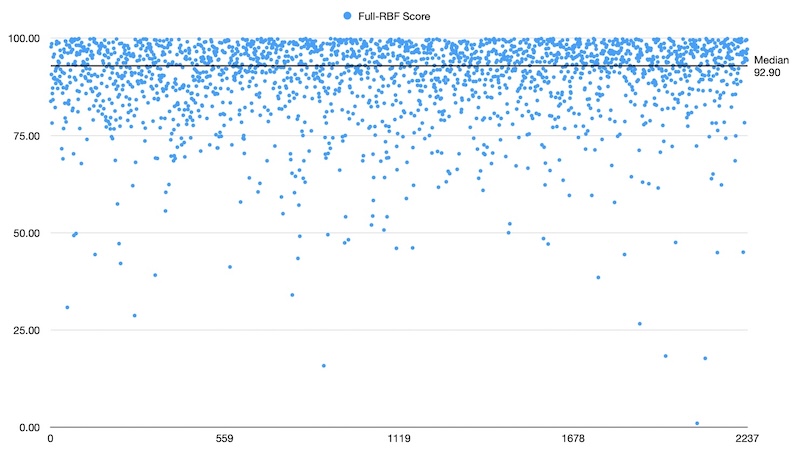
To refresh, we’re asking whether running -mempoolfullrbf as a default policy is a better predictor of next-block contents than not. I use a metric P2P Score as an indicator of the degree of similarity between a node’s current block template and the next confirmed block.

One difference between this round and the previous is that we reduced the block template interval from 5min to 3min. Additionally I’ve added a column for block fees to the raw data set, as I thought it might be interesting to study trends between fees and block time, fees and score, etc (but those results aren’t in yet).

Results

These are scatterplots of ~2000 data points in each test between heights 827650 and 856176.

Discussion

The sample means were so strikingly similar that I didn’t bother applying any statistics to them. I did however conduct a 1-way analysis of variance (ANOVA) to test a suspicion that the fullrbf node experienced less variance in score.

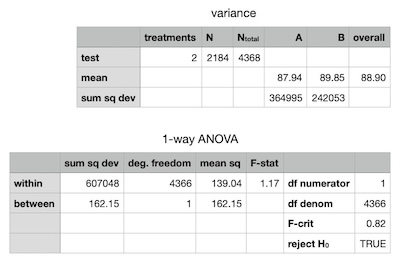
An obvious confounding variable was node uptime which could affect network visability. The fullrbf node is an always-on server while the bip125 node is a pruned node on an old laptop that is off most of the time. I attempted to smooth out that variation by making sure the nodes were peered with one another giving them the opportunity to share their own mempool contents.

One of the reasons I took on this exploration was to engage in a larger discussion about the health of the p2p network. It’s important that node operators have a habit of monitoring statistics to track changes in usage by network participants.

The score is intentionally “dumb”. We would like it to have a value close to 1, but deviations from perfect aren’t necessarily a cause for concern. Indeed we expect to see variation by virtue of the distributed network - some nodes see some transactions and other nodes see others. It would be unrealistic to expect perfection from every block - certainly that would make it less useful as a metric. Thankfully I was surprised to observe such high p2p scores on a regular basis. In contrast, witnessing large or prolonged deviations could be a sign that either 1) local policy has fallen adrift of the wider network or 2) significant volumes of transactions are confirming having never entered the mempool to begin with.

In terms of policy I don’t take a stance on whether nodes should conform to miner practices or vice versa. I do think we should try to strike a balance between sane and reliable defaults while recognizing the need to evolve and adapt policy with the aim of making the mempool an efficient place where users will want to transact.

Resources

• policy: enable full-rbf by default #30493
• ValuedMammal/mempool-util

---

Evaluating the predictiveness of block composition under variable relay policy

Here are some early results of a study in progress that seeks to compare the accuracy of anticipated transaction data in newly confirmed blocks under different policy conditions. The available data thus far represents a trial run of the experimental methods. Plans are underway to expand the scope of analysis in the coming months.

Question:

Will a bitcoin node configured with mempoolfullrbf see more of its pool of unconfirmed transactions be included in the next block than a node running the default configuration?

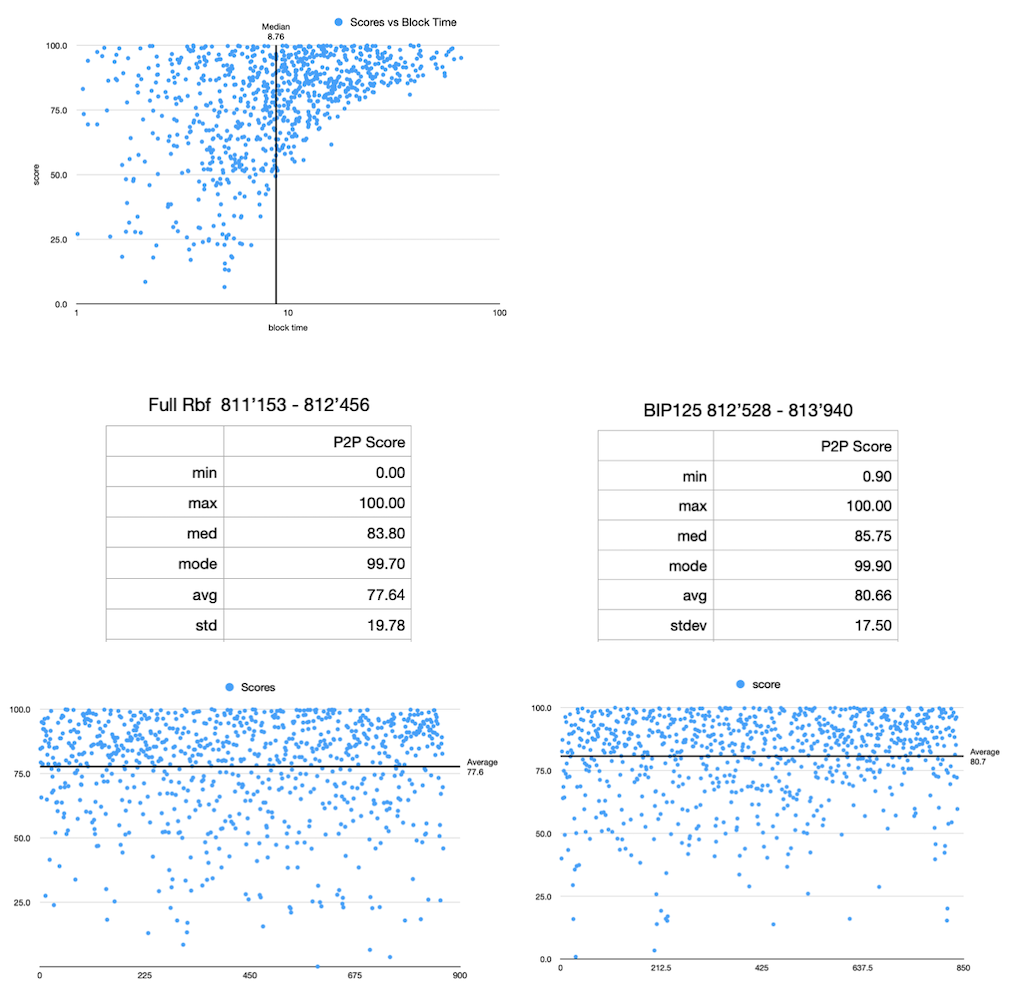
At first glance, I don’t see much difference in the two samples, though I’d say it’s far from conclusive for reasons I’ll mention shortly, but overall I’m pleased to have implemented the chosen methodology.

In each of the two test cases, we captured the node’s view of the mempool using bitcoind’s getblocktemplate RPC, and this was repeated at 5 minute intervals. The result of getblocktemplate is, as the name suggests, a template for a consensus-valid block containing a set of transactions the node considers candidates for block inclusion. An interval of 5 minutes was chosen because it’s less than the average block time of 10 minutes, so it’s relatively certain we would create a new template at least once per block.

When a new block arrives, we compare the transaction data in the newly confirmed block to those present in the most recent block template. We then quantify the degree of similarity using a metric dubbed the P2P Index Score following a simple formula:

score = (actual - unseen) / actual

where unseen is the number of transactions occurring in the actual block and not in the projected block. Hence, score is a number between 0 and 1, with 1 representing perfect similitude, expressed as a percent as shown in the accompanying figures. The set of scores were filtered to exclude obviously invalid ones. For example, if the duration between two consecutive blocks is less than the configured block template interval, the last block template will have been rendered stale upon scoring the first block, and hence the computed score for the second block should be discarded. That’s the gist as far as methodology.

Without commenting much on the data, I would direct your attention briefly to the top figure plotting score vs block time. We see the data is noisy below a time of ten minutes, but we see a positive correlation emerge as block times grow longer than the average. While unrelated to mempool policy, this serves to build an intuition that a longer block time affords unconfirmed transactions ample time to propagate and thus a greater chance they’ll be represented in the projected block. Similarly for the scatterplots of block score, the relative density of data above the 50% line is reassurance that the node has a somewhat accurate view of the space of unconfirmed transactions, and that there may yet be insights to glean.

There were some flaws (or at least nuances) in the execution that deserve to be mentioned:

1) The two datasets weren’t run side-by-side as is evidenced by the block ranges. A more robust study should control this.

2) The meaning of unseen in the formula for score is nuanced. A transaction found in an actual block that wasn’t previously projected may still be present in the local mempool, hence it was technically seen by our node - it just didn’t make it into the next block. More context is needed to determine the cause of the discrepancy.

3) No attempt was made to control the number or type of peer connections made. I will say in the fullrbf scenario, an attempt was made to ensure we had at least one fullrbf peer, but in fairness, perhaps that should have been done for both scenarios. In general I’m not sure we should try to tightly control the quality of connections, as they can be handled automatically while requiring no input from the user. At the very least we should ensure the connection count doesn’t drop so low as to risk being cut off from normal relay activity, and if the bip125-enforcing node allows a certain connection type (tor, i2p, etc), then the same configuration should be mirrored on the fullrbf node. An approach at the other extreme would have us make only manual connections to the same group of peers in each scenario. This option may be considered for future trials.

4) As noted in the methods primer, we discarded scores for a block that arrived below the refresh interval of 5 minutes, however implementing the criteria that would uniformly filter invalid data is nuanced. For instance, imagine the duration between two blocks is 2 minutes: since this is less than the defined template interval, we assume the result should be dropped. But what if a new template is crunched at minute 1, i.e. one minute after the arrival of the first block and one minute prior to the arrival of the next? In this case we should keep both scores. Sometimes blocks arrive only seconds apart. How small a range should be allowed before considering it “too soon” to compute a score for the second block? I’m open to ideas for improvement here. From the small amount of data available, we can already see the range of block scores spans all possible values making it difficult to spot outliers and leaving little indication that an invalid point might stand out from the rest.

To make matters worse, it turns out there is no optimal duration for the template refresh interval that minimizes invalid results. Early on, I naively envisioned block times spread over a normal bell curve, and that taking the time at say 2 standard deviations below the mean would capture the bulk of the data we’re interested in. In fact the distribution of block time is anything but normal, because the standard deviation of block time is the average block time, i.e. 10 minutes. In statistics this pattern is characteristic of what’s called an exponential distribution. In bitcoin, it comes as a consequence of pure probabilistic block times and, being the unrefined statistician, is something I was enlightened to learn.

Lastly, the next iteration of the study should include much more data, which entails letting the collection phase run (ideally uninterrupted) for an extended time. The raw data set from the trial run included around 1000 blocks in each scenario. A more robust dataset should include perhaps 10 times that much. Further, consider that 1000 blocks is only about half of one difficulty period. If the experiment were run over the course of say 6 months (even intermittently, as long as both nodes are collecting at the same times), then we’d have more opportunities to gather a variety of data across different mempool regimes.

Raw data
fullrbf.csv
bip125.csv

How to verify a signed message using Sparrow

1) Download Sparrow for desktop. Open the app. 2) Go to Tools -> Sign/Verify Message 3) Fill in the address, message, and signature. Click ‘verify’. The result is that the signature is either valid or it’s not.

Example
—–BEGIN BITCOIN SIGNED MESSAGE—–
Send sats here!
—–BEGIN BITCOIN SIGNATURE—–
bc1qg35sdfjkpk9dwcxmx9t8qmnju9cl8g42cnry50
J1MaTfrU2S7btQVXEVpikNpxe/XNK/DFzWN5USIXaSGdDryLHN9fOiJD4VGFTlpPSrkMU1n0Ln4kzKyix8bXQP4=
—–END BITCOIN SIGNATURE—–

Why is this important?
A valid signature shows that the entity who signed the message controls the keys associated with the address, and it gives the sender some confidence they’re not sending sats into a black hole. Likewise, you should be extremely skeptical of an entity who claims to control an address but is unable to produce a signature. Not your keys, not your coins.

How does it work?
Bitcoin relies on public key crypto which is asymmetric, meaning keys come in pairs of private/public keys. The public key is derived from the private key. To serve as an effective signing scheme, signatures need to be difficult or impossible to forge, yet trivial to verify. To produce a signature, the signer finds a random point on the elliptic curve and computes a proof that is a function of the nonce, the message hash, the EC point, and the priv key. If the verifier can recover the same EC point using the signature and the pubkey, then the signature is deemed valid.

updated: 4Feb 2024